Элементарные финансовые расчеты
Например, предприятие может столкнуться с необходимостью выбора между получением кредита на 5 месяцев под сложную номинальную ставку 24 % (начисление процентов поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком погашения. Небходимо определить простую учетную ставку, которая сделает учет векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26) получим d = 22,21 %.
Кроме формул, приведенных в табл. 2.2.2 и 2.2.3, следует отметить еще одно полезное соотношение. Между силой роста и дисконтным множителем декурсивных процентов существунт следующая связь:
![]() . (2.2.38)
. (2.2.38)
Таблица 2.2.2
Эквивалентность простых ставок
| Простая процентная ставка (iпр) | Простая учетная ставка (dпр) | |
| Сложная процентная ставка (iсл) | | |
| Сложная номинальная процентная ставка (j) |
(2.2.25) | |
| Сила роста (d) | | |
| Простая учетная ставка (dпр) n = t/K | | – |
| Простая учетная ставка (dпр) ki = kd = 360 | | – |
| Простая учетная ставка (dпр) ki = 365 kd = 360 | | – |
Таблица 2.2.3
Эквивалентность сложных процентных ставок
| Сложная процентная ставка (iсл) | Сложная учетная ставка (dсл) | |
| Сложная номинальная процентная ставка (j) | | |
| Сила роста (d) | | Сложная номинальная процентная ставка (j) |
| | ||
| Сложная учетная ставка (dсл) | | – |
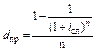 (2.2.22)
(2.2.22) 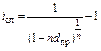 (2.2.23)
(2.2.23) 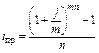 (2.2.24)
(2.2.24) 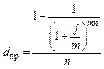 (2.2.26)
(2.2.26) 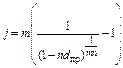 (2.2.27)
(2.2.27) 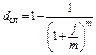 (2.2.41)
(2.2.41) 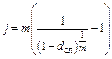 (2.2.42)
(2.2.42)